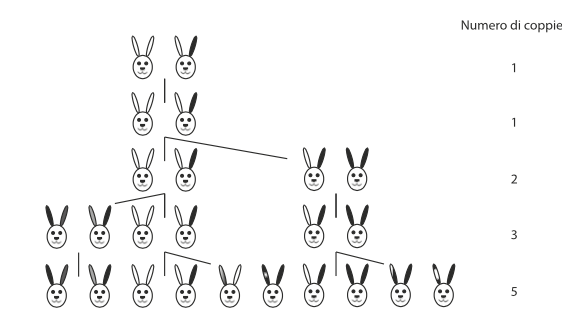
1, 1, 2, 3, 5, 8…
sono i primi numeri della successione elaborata dal matematico Leonardo Pisano, detto Fibonacci, per descrivere la crescita mensile di una popolazione di conigli, supponendo che gli animali diventino fertili al compimento del primo mese e che ogni coppia di conigli partorisca al compimento del secondo mese.
È difficile esagerare la portata del fascino e del senso di mistero che questi numeri accendono. L'autrice lo mette in chiaro già a pagina 1: «Perché di numeri di Fibonacci è piena la storia dell’arte, oltre che quella della matematica, e se state leggendo questo libro è sicuro che questo nome l’avete già incontrato e vi incuriosisce».
E più avanti: «parlare di numeri di Fibonacci equivale a parlare di sezione aurea. Facciamo infatti qualche divisione: a partire dal secondo 1 nella successione, dividiamo ciascun numero di Fibonacci per il numero che lo precede. Otterremo in questo modo i seguenti quozienti:
1/1=1; 2/1=2; 3/2=1,5; 5/3=1,67; 8/5=1,6; 13/8=1,625; 21/13=1,615; 34/21=1,619, …
A mano a mano che i numeri crescono, il risultato delle divisioni si avvicina sempre di più a 1,618, l’approssimazione della sezione aurea».
Le orme di Fibonacci si possono ripercorrere nella passeggiata pisana: una vera «matematica dei miracoli!».